本文从blog.163.com/kazenoyume@126/上迁移过来

最近在工作之余，参加了hihocoder推出的编程提高班。这个编程提高班真的很有意思，它的讲课内容是跟算法分析设计有关的。而这周讲课的内容，是大家都耳熟能详的KMP算法。
在大二的时候，我曾经学习过KMP算法，当时还刷了好几道OJ题，所以就理所当然的以为这周的算法题目是相当的简单，不需要花很多时间就能完成的了。但是当我开始做题目的时候，我却发现自己完全不懂KMP算法！当初学习KMP算法的时候，只是对算法有个直观上的了解，就只知道它的时间复杂度和空间复杂度，完全只把它当作API来用。而且当时学习的时候也是晕头转向的，总觉得KMP算法绕得太厉害了，一时半刻学不来，于是就没学了。
在写之前，我参考了好网上好几篇写KMP算法的文章。那些文章内容始终都觉得有点饶，不太适合自己的理解。但是自己又觉得自己还没有能力把这个算法说得清楚明白，简单明了。我想了下，既然别人的文章都叫做《详解KMP算法》，那我给自己的文章起个名字叫做浅尝KMP算法吧。要是大家看完之后，觉得还是没理解KMP算法的话，那我能说：“这只是浅尝KMP算法啊，不懂也很正常啊，大家就当是被我忽悠进来的吧:)”。

KMP算法介绍

给定两个字符串A和B，怎么样判断B是不是A的子串呢？
这问题相当简单，相信每一个学过编程语言的人都知道怎么解决这个问题。最简单的做法，就是粗暴(Brute Force，下文称为BF)的枚举A的所有可行下标i, 判断A[i, i+B.len-1]和B是否相等（B.len为B字符串的长度）。假设A和B的字符串长度分别为A.len和B.len，那么这种算法的时间复杂度为O(A.len * B.len)。当A和B比较小的时候还可以接受，但是当数据量比较大的时候效率就很低了。为了提高字符串的匹配算法，以前的计算机科学家们可真是前赴后继，集体跳坑研究出各种字符串算法，比如大名顶顶的trie tree。今天我们要介绍的主角可不是它，而是KMP算法。
KMP算法的全称是Knuth-Morris-Pratt，这三个英文单词是研究出这个算法的这三个大神的名字。相信大家对Knuth也不会陌生，他就是《计算机程序设计艺术》一书以及排版软件Tex的作者。而Morris是函数式编程思想的开山鼻祖之一，比如最近很流行的惰性计算就是它提出的。Pratt是Knuth的弟子，但是最牛逼的是他仅用了20个月就把博士学位拿到手了，简直是个天才啊。 KMP算法的核心思想是通过空间效率来换时间效率，它在进行字符串A和B匹配之前，需要先计算出B的一些特性，然后根据这些特性来优化匹配算法。KMP算法的时间复杂度是线性的，听起来非常诱人是不？

初探KMP

包括笔者在内，我相信大家在看网上的KMP算法时也是看得不太懂，总是云里雾里的，觉得这东西很悬乎。我在这篇文章里想给大家一个对KMP算法的初步印象，给大家一种感觉，希望大家在看完这篇文章后觉得，其实KMP算法也不难啊～ 刚才也说过了，BF算法正是由于过多地比较这些重复出现的字符串导致其效率比较低。假如在比较A和B字符串之前，我就知道哪些字符应该比较，哪些字符不应该比较，减少BF中重复比较字符串的次数，效率就自然提高了。 比如A=abababababb，B=abababb，BF需要进行的比较计算如下所示：
1.jpg
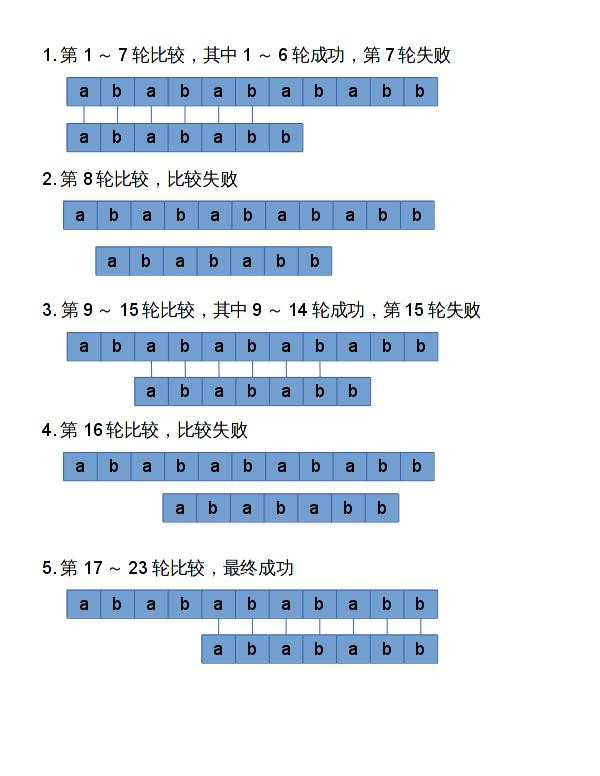
在上面这些比较里面可以看到，A和B的比较要不就是只差最后一位比较就成功了，要不就是完全不成功。而且A和B的比较过程中，第1～6轮 和第9～14轮和17～22轮的比较是非常相似的。那么我们是否能利用这些信息，在不匹配的时候让B向右位移一定的步数，使得A和B重新有部分匹配呢？利用这些信息来使B进行跳跃的就是KMP的核心思想了。

NEXT数组

在第二章中，说明了KMP的主要思想是利用字符串B自身的信息，在匹配的时候进行跳跃。保存这个匹配信息的就是NEXT数组。这个NEXT数组真的很作弊，它作弊的地方就在于，当它发现A和B不匹配的时候，它知道应该把B向右移动多少位来重新匹配。比如上面的例子中，B=abababb的NEXT数组是{0, 0, 1, 2, 3, 2, 0}。现在我们利用这个数组配合来讲解一下上面的KMP算法演示的例子。
在第1～6轮时，A和B字符串均匹配成功了。但是在第7轮的时候却失败了，当第7轮匹配失败的时候，应该去查阅NEXT[6]，发现B字符串需要向右位移2位，此时位移两位之后，A[3, 6]和B[1, 4]还是匹配的。

        A=abababababb
位移前	B=abababb
位移后	B=__abababb

那么第8轮的时候就去比较A[7]和B[5]，第9轮的时候比较A[8]和B[6]。当在第10轮的时候，发现A[9]和B[7]无法匹配，这时候继续查阅NEXT[6]，将B字符串继续向右移动两位。移动两位之后，A[5, 8]和B[1,4]还是匹配的。

        A=abababababb
位移前	B=__abababb
位移后	B=____abababb

这时候继续进行匹配，直至匹配成功。
那么这个NEXT数组到底是什么呢？为什么能这么神奇呢？
一种合理的对NEXT数组的解释，是最长公共前后缀的数目。最长公共前后缀指的是，对于一个字符串S来说，找出最大的i，使得S[1, i] == S[S.len - i + 1, S.len]（1 < i < S.len）。这里，S[1, i]指的是这个字符串的一个前缀，S[S.len - i + 1, S.len]指的是这个字符串的一个后缀。在知道NEXT数组数值的前提下，当发生字符串A和B不匹配的情况，就可以将B字符串向右位移<A和B已成功匹配字符串数目 - NEXT[A和B已成功匹配字符串数目]>这么多位。
网上基本上对NEXT数组的解释少之又少，在下一小节中，我尝试提出我自己的愚见。要是大家赶着用这个算法的话，那这一小节就可以跳过了吧。

NEXT数组的解释

我们再来重新看一下BF算法那个例子。并将所有成功匹配的地方凑起来，看看到底是什么。
2.jpg
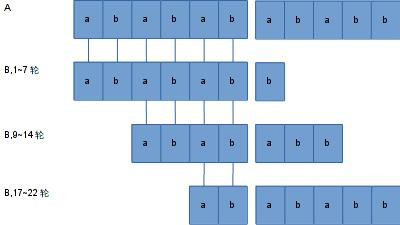
在上图中，我把A和B两个字符串在第7轮比较中不匹配的地方劈了开来。可以看到在左面，当发生匹配成功的时候，第1～7轮的B和第9～14轮的B有公共字符串的部分，而且它也与第17～22轮的B有公共字符串的部分。当没有发生匹配成功时，它们之间没有公共的部分。那就是说，在劈开点之前，假如想通过向右移动B，来使A和B再次发生匹配在劈开点之前完全匹配的话，需要满足:
（1）设B和A已成功匹配了i个点，不匹配的地方是i + 1
（2）设j为将B向右移j步时，能使B和A在不匹配的地方之前有重新匹配的部分
（3）B[j + 1, i] == B[1, i - j]
（4）0 < j < i（0步时没有意义，i步时已经完全超过了劈开点，也没有意义)
在上面例子中i = 6, j = 2或4。此时，它们与A的公共匹配数分别为4和2。上述条件中的第3项中，B[1, i - j]是B[1, i]的一个前缀，B[j + 1, i]是B[1, i]的一个前缀。换句话说，第3点实际就是找出字符串B[1, i]的公共前后缀，j就是代表这个公共前后缀的长度。假如有了这个j，我们就可以知道B应该向右移动多少位了。

现在来思考一下为什么NEXT数组选择的是最长公共前后缀。假如一个字符串遇到了多种可行的跳跃方案时，比如上面例子（A=abababababb，B=abababb，i = 6, j = 2或4）这时候该如何选择呢？答案是选择j较小值者进行位移。
一种直观的解释，就是j是选择较大者进行位移的话，那么在位移过程中将会丢失一些有用的信息。当B从ababab的已匹配状态跳跃到ab的已匹配状态时，明显跳过了abab的已匹配状态，那么假如这时候遇到的A字符串不是abababababb，而是ababababbab，那匹配就失败了，显然选择大的进行跳跃的是不对的。
另外，选择较小的j进行位移的话，当下一步匹配失败的时候，还是可以迁移到选择较大的j进行位移的状态的。当存在有两个的j值j1和j2(j1 < j2)的时候，那么就会有以下两个条件成立：（1）B[1, j1] == B[i - j1 + 1, i]（2）B[1, j2] == B[i - j2 + 1, i]。我们把这两个条件画个图，就知道为什么选择较小的j也可以迁移到选择较大的j的状态了。

3.jpg
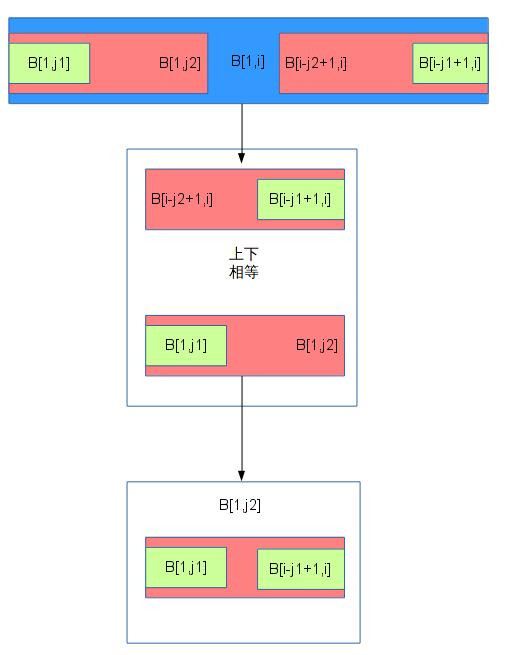
当发生位移后，A和B匹配的字符为B[1, j2]。从图中可以看到，其实B[1, j1]的完全就是B[1, j2]的公共前后缀里面的前缀，当B[j2 + 1]和A再次发生不匹配的时候，B完全是可以迁移到B[1, j1]和A匹配的状态的。至此，证明了选择较小的j的有效性，也证明了为什么NEXT数组记录的是最长公共前后缀而不是随便挑一个数了。（当j有超过两个以上的时候证明类似，当j1<j2<j3<…<jn时，每次只证明相邻的两个即可）

至此，总结了KMP如何使用NEXT数组的方法，KMP的主函数就可以写出来了:

METHOD KMP:
j = 0 #A和B已成功匹配的字符串数目
FOR i = 1 TO A.len:
    WHILE j > 0 && A[i] != B[j + 1]: j = NEXT[j]
    IF A[i] == B[j + 1]: ++ j
    IF j == B.len: j = NEXT[j] #已找到匹配的地方，重新匹配

NEXT数组的计算

刚开始时，笔者也只是想到O（n^3)的算法。但是看了网上的各种讲解之后，才发现它是一个递推问题。
NEXT数组的计算是这样的，要计算NEXT[i]时，可利用NEXT[1]，…， NEXT[i-1]的信息进行计算。考虑NEXT[i]和NEXT[i-1]，有以下几种情况：
（1）NEXT[i - 1]不存在(NEXT[i - 1] == 0)，若B[1] == B[i] (i != 1)时，NEXT[i] = 1，否则为0。
（2）NEXT[i - 1]存在，且B[1, NEXT[i - 1]] == B[i - NEXT[i - 1], i - 1]，此时，若B[NEXT[i - 1] + 1] == B[i]，即说明B[1,i]的最长公共前后缀可以从B[1,i-1]计算而出，此时NEXT[i] = NEXT[i-1] + 1。
（3）NEXT[i - 1]存在，且B[1, NEXT[i - 1]] == B[i - NEXT[i - 1], i - 1]，但B[NEXT[i - 1] + 1] != B[i]。此时，即说明无法通过扩展B[1, i-1]的最长公共前后缀来计算出NEXT[i]。
第一和第二种情况都比较好理解，而第三种情况理解起来可能就比较麻烦了。
4.jpg
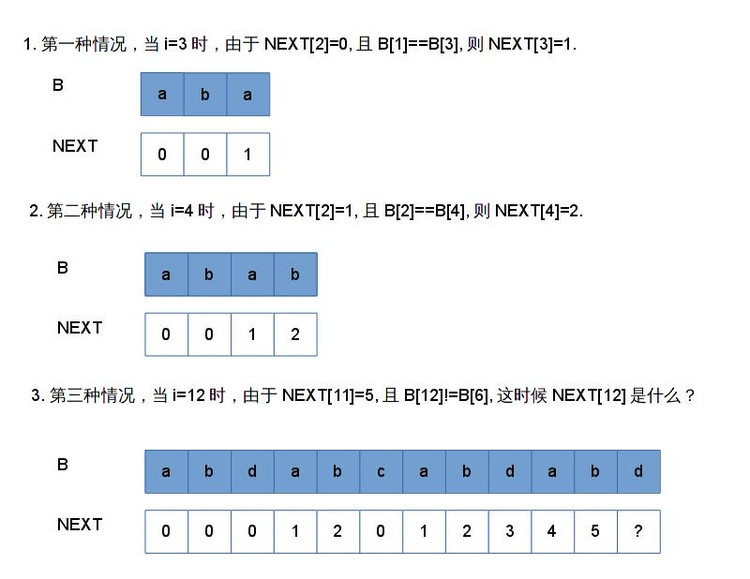
下面我以B=abdabcabdabd为例子，讲解第三种情况的时候该如何计算NEXT数组。
当i=12的时候，NEXT[11] = 5，但是由于B[12] != B[NEXT[11] + 1]，无法把第2种情况应用上去。当发生这种情况的时候，B[1,12]的最长公共前后缀串必然不会比NEXT[11]大，否则将不会出现这第3种情况。现在可以知道B[1,12]的最长公共前后缀串必然在[1, NEXT[11]]这个区间。倘若要找出一个k，使得B[1, k]和B[12-k+1, 12]相等，这个i就必然会落在[1,NEXT[11]]这个区间。在这个例子中，这个k为3，我们来看看当k=3的时候，到底发生了什么神奇的事情。
5.jpg
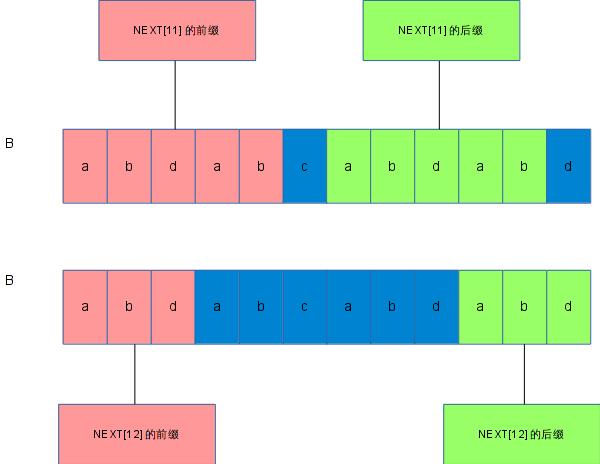
从上图可以看出，B[1,11]和B[1,12]的最长公共前后缀有公共的部分。NEXT[12]的前缀与NEXT[11]的前缀有公共的部分，NEXT[12]的后缀又和NEXT[11]的后缀有公共的部分。倘若抛开NEXT[12]中的d，将其染成灰色，再来看看是怎么样的。
6.jpg
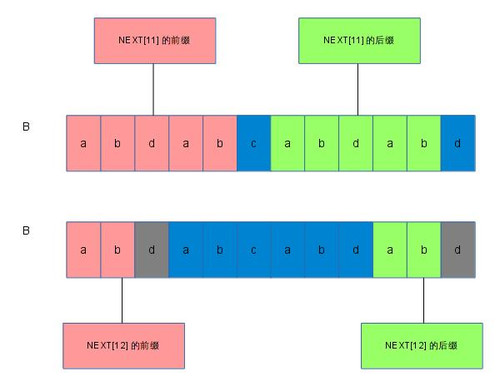
现在可以看到，除去d这部分，NEXT[12]的后缀是包含在NEXT[11]的后缀里面的。由于NEXT[11]的前缀和后缀是相等的，即B[1,5]=B[7,11]，所以NEXT[12]的后缀（去除d部分)完全可以在B[1,5]字符串的后面几位找到。NEXT[12]的前缀（去除d部分）也可以从NEXT[11]的前几位找到。假如去除d部分的话，NEXT[12]所找的公共前后缀是在NEXT[11]的前缀里面找的。同时，我们在找k的时候，总是希望k尽可能的大，即B[1,12]的公共前后缀尽可能的大，也就是找出B[1, NEXT[11]]里面的最长公共前后缀。
当找到B[1, NEXT[11]]的最长前后缀的时候，也就是找到NEXT[NEXT[11]]的时候，就需要判断B[NEXT[NEXT[11]] + 1]是否与B[12]相等，当相等的时候，NEXT[12] = B[1, NEXT[11]]中最长公共前后缀的数目 + 1 = NEXT[NEXT[11]] + 1。当不相等的时候，其实问题又再次转化回了第三种情况，只是此时借助的信息不是NEXT[11]，而是NEXT[NEXT[11]]。
KMP构造部分伪代码如下：

METHOD compute_prefix
NEXT = array of size B.len
NEXT[1] = 0
FOR i = 2 TO B.len
    j = NEXT[i - 1]
    WHILE j > 0 && B[i] != B[j + 1]: j = NEXT[j]
    IF j > 0: NEXT[i] = j + 1
    ELSE：NEXT[i] = B[i] == B[1] ? 1 : 0

在这里，对于第（1）和第（2）种情况来说，它们都能直接跳过代码中第五行的判断条件，从而直接到达最后的IF-ELSE判断。其中IF对应的是第（1）种情况，ELSE对应的是第（2）种情况。至于第（3）种情况，就需要在循环中作一定的处理后再作判断。

六. 结尾

好了，说了那么多废话终于写完了。第一次体会到写技术文章是多么辛苦，以前一直是做伸手党，以后要多写技术博客才行～

参考资料：