最近在算法课上,遇到了一个很有意思的题目,题目的大意是寻找空间中的最近点对。
给定空间上的n个节点,如何查找这n个点对中最近的点对的距离?
这里的距离采用欧氏距离
朴素法
朴素法是最为简单和粗暴的办法,具体思想是枚举空间中所有可能的点对,并且分别计算这些点对之间的距离。这些点对之间的最小距离即是答案。
朴素法需要分别枚举i和j,算法的时间复杂度为。
分治法
分治法的基本思想是将一个问题分解成几个更小的子问题,求解并合并这些子问题作为这个问题的结果。当子问题足够小的时候便可以直接求解。因此,分治法的解法分为两个步骤,分解和合并。
分解
我们的问题是求解这n个节点中的最近点对,那么如何该分解这个问题让其成为更容易求解的问题呢?一种直观的思想是在空间中划出一条线,让这条线把这个空间划分成两个部分。此时,原问题的空间便成为了两个更小的空间。
这条线的选择是有技巧的,我们希望这条线能将这n个点等分成两份,使两个子问题的规模尽量相等。若将这n个点都投影到X轴上,便可以发现这条直线可以是x=(这n个点的中位数),此时这条直线很好地将原来的数据等分成了两份。
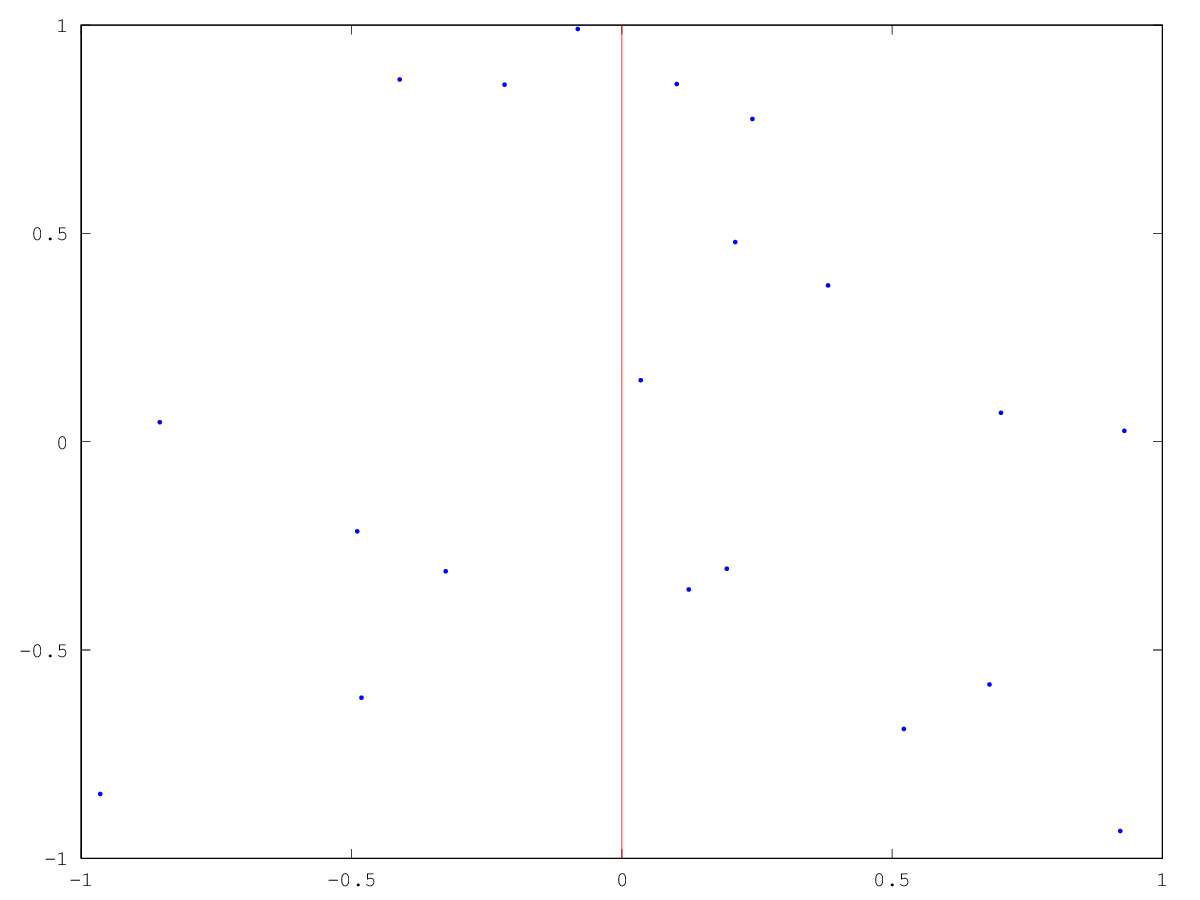
至此,我们就把数据分成两等分了,同时也将原问题化成两个更小的问题。不断应用分解的思想,将数据变得更加的小。当小问题的数据规模为1或者2的时候,这个问题就很容易解了。当数据规模为1的时候,由于这个空间没有点对,所以应该返回一个距离的最大值。而当数据规模为2的时候,直接返回这两个节点之间的距离即可。
合并
当求得子问题的解后,就该考虑如何合并这些解。假设现在这个问题的输入数据集合为,两个子问题的输入数据集合分别为和。那么这两个子问题求得的解为在和空间上的最小距离。
对于来说,其最小距离点对只可能是以下三种情况之一:
- 最小点对的两个点均在里,因此原问题的解为子问题的解。
- 最小点对的两个点均在里,因此原问题的解为子问题的解。
- 最小点对的一个点在里,另外一个点在里。
为了说明方便,现设,。
对于前两种情况,我们只需将设答案。
第三种情况出现时,必然有。由于一个节点在中,一个节点中,并且他们之间的距离比小。所以在中的节点必然在中,在中的节点必然在中。同时对于的节点,如果在中存在节点,使得,则q必符合这个条件。对于点,我们只需比较符合上述条件的点即可,从理论上可以证明,对每个节点,只需比较6个节点便可得到解。
此时,算法的计算步骤如下:
- 求解和两个子问题,并设。
- 查找在中的所有符合的节点集合,查找在中的所有符合的节点集合。
- 对在中的每个节点,执行
查找中所有符合的节点q,更新。 - 即是该范围中的最小点对结果。
限制范围证明
对于合并问题的第三种情况,中的每个节点最多只需要搜索中的六个节点。本节将用于证明该推论。
要证明该推论,先引入鹊巢原理:
若有n个笼子和n+1只鸽子,所有的鸽子都被关在鸽笼里,那么至少有一个笼子有至少2只鸽子。
鹊巢原理的另外一个表达是,若有n个盒子和n+1个球,所有的球都在这些盒子里面,那么至少有一个盒子有2个球。
对中的其中一个点,作,,,这四条直线围成的矩形。此时,这个矩形的大小为。将这个矩形横切成两等分,再竖切成三等分,得到六个大小为的小矩形。
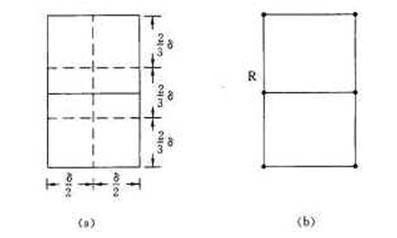
我们利用反证法来证明这个区域中最多只有6个节点,假如这个矩形区域中存在7个或以上的点,由鹊巢原理可以知道其中一个小矩形必然至少有2个点。而小矩形中,两个点的最远距离为。此时该距离比小,由于这些点都是在中,并且,则此时发生了矛盾。因此,原假设成立。
算法复杂性
对于一个数据规模为n的最近点对问题,定义它的复杂度为。
- 算法的第一步将问题分解成两个子问题,分解这部分的复杂读是。
- 第2步线性扫描,上界为。
- 第3步对于P中的每一个点,其比较的时间复杂度是常数。由于需要扫描所有P点,上界为。
原问题时间复杂度。使用算法导论的主定理可以得出总的上界为
算法实现
这个算法在实现时有几处小trick:
- 由于每个问题需要快速地查找划分该问题的线段,所以可以先对以x排序,得到数组。取中点时也常常不取中位数,而取中点,这样可以忽略很多特殊情况。
- 在实际实现中,经常忽略和的区别,将两个集合中的节点视为等价的。在比较的时候直接比较这个集合中的节点。(理论上可以证明合并后的集合,每个节点最多比较8次,但笔者还没会如何证明)
- 对于每个问题的节点,需要快速地查找在y轴上符合范围的节点。因此,需要每一步中的数据以y排序。由于该问题跟归并排序的分解十分的像,所以可以在求解完子问题时对数据根据y轴进行归并排序。
C++版本实现代码如下:
#include <stdio.h>
#include <string.h>
#include <math.h>
#include <algorithm>
class CloestPair {
private:
struct Point {
double x, y;
};
static const double kMaxDist = 1e20; // 原问题最大可行距离
int size_;
Point *S_; // 原集合数组
Point *Z_; // 辅助数组,用于存储中间结果
// 计算两个点欧拉距离
static double GetDist(const Point &p ,const Point &q) {
double s = (p.x-q.x)*(p.x-q.x) + (p.y-q.y)*(p.y-q.y);
return sqrt(s);
}
static double Min(double a, double b) {
return a < b ? a : b;
}
static bool CompByX(const Point &p, const Point &q) {
return p.x < q.x;
}
//对S_[start, mid]和S_[mid + 1, end]部分进行归并
void Merge(int start, int end) {
int mid = (start + end) / 2;
int i = start, j = mid + 1;
int idx = start;
while (i <= mid && j <= end) {
if (S_[i].y < S_[j].y) Z_[idx++] = S_[i++];
else Z_[idx++] = S_[j++];
}
while (i <= mid) Z_[idx++] = S_[i++];
while (j <= end) Z_[idx++] = S_[j++];
for (int i = start; i <= end; ++ i) S_[i] = Z_[i];
}
double GetMinDist(int start, int end) {
// 子问题足够小,可解
if (end - start <= 0) return kMaxDist;
if (end - start == 1) {
Merge(start, end);
return GetDist(S_[start], S_[end]);
}
// 取出划分点
int mid = (start + end) / 2;
double mid_x = S_[mid].x;
double left_val = GetMinDist(start, mid);
double right_val = GetMinDist(mid + 1, end);
double min_val = Min(left_val, right_val);
// 将数据以y进行排序,方便查询
Merge(start, end);
// 找出所有在[mid - theta, mid + theta]的点
int z_count = 0;
for (int i = start; i <= end; ++ i)
if (mid_x - min_val <= S_[i].x &&
S_[i].x <= mid_x + min_val) {
Z_[z_count++] = S_[i];
}
// 对每个点p,找出在其范围内的点q
for (int i = 0; i < z_count; ++ i)
for (int j = i + 1; j < z_count; ++ j)
if (S_[j].y - min_val <= S_[i].y) {
double dist = GetDist(S_[i], S_[j]);
min_val = Min(min_val, dist);
} else break;
return min_val;
}
public:
CloestPair(int size) {
size_ = size;
S_ = new Point[size];
Z_ = new Point[size];
}
~CloestPair() {
if (S_ != NULL) delete[] S_;
if (Z_ != NULL) delete[] Z_;
}
void Input() {
for (int i = 0; i < size_; ++ i)
scanf("%lf %lf", &S_[i].x, &S_[i].y);
}
double CalMinDist() {
// 为方便找中点,先对x排序
std::sort(S_, S_ + size_, CompByX);
return GetMinDist(0, size_ - 1);
}
};
int main() {
int n; scanf("%d", &n);
CloestPair cp(n);
cp.Input();
printf("min dist: %lf\n", cp.CalMinDist());
return 0;
}
参考资料: