论文简要思想

在论文中，它定义了两个比较重要的公式，$\rho和\delta$。

$\rho_i = \sum_j{\chi(d_{ij} - d_c)}$。其中，$\rho_i$代表的是离节点i距离少于$d_c$的节点个数，$d_c$也称为截断距离。由于$\rho_i$能代表节点所在位置附近节点的分布密集情况，因此它也称为节点i的局部密度。

$\delta_i = \min_{j: \rho_i > \rho_j}(d_{ij})$。$\delta_i$的具体意思是，先找出比自身局部密度大的节点，在这些节点中选择离节点i距离最短的值作为$\delta_i$的值。

在计算出所有节点的$\rho$和$\delta$后，将在二维平面上画出$(\rho, \delta)$的值。画出这些值的图叫做决策图。用户依赖决策图来进行聚类中心的选取。下图种，左图为需要聚类的节点，右图为决策图。

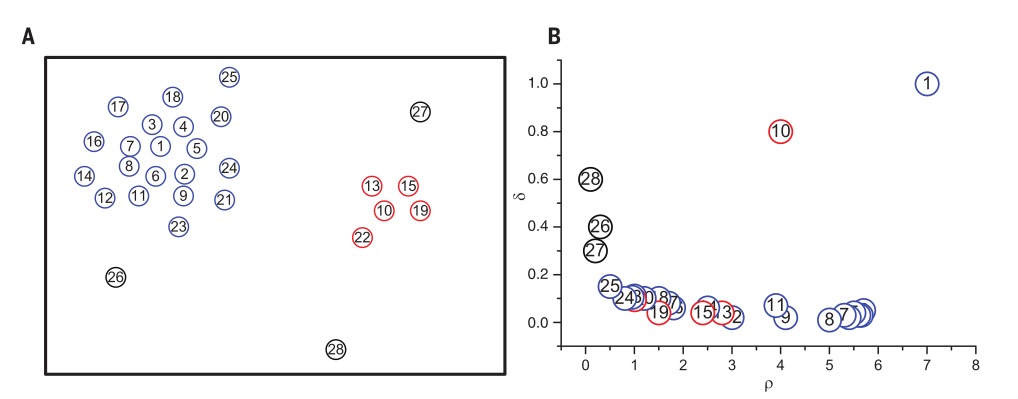
在画出决策图后，需要用户根据决策图选择聚类中心。文章提出了一种基于主观印象的启发式方法，靠用户的主观印象选择$\rho$和$\delta$都较大的节点作为聚类中心。文章认为只有当$\rho$和$\delta$都较大的时候，它才能代表聚类中心。因为要成为聚类中心，其局部密度必须较大。而当某节点$\delta$较小的时候，由于该节点附近有一个局部密度比其大的节点，因此它不能成为聚类中心。

在选出了聚类中心后，对每个节点，找出离其最近的局部密度比其大的聚类中心，这个聚类中心所属的类就是该节点所属的类。

实现细节

在实现过程中，发现若只使用论文中的$\rho_i$的定义做的话，聚类的效果会非常的差，只有在合理选择$d_c$时聚类效果才比较好。导致这种现象有两种原因，一是它只考虑了截断距离，并没有考虑到在阶段距离中的点对局部密度的贡献。另外一个原因是$d_c$的选择非常依赖与数据集中的相对距离大小。因此，在这里，我依照原论文中实验部分所采取的公式，将两节点的空间距离映射到了gaussian kernel中去。并且修改了一下$\rho_i$的计算公式。作这种修改的想法是，若空间中的两点越近，其局部密度贡献值应该越大。

$$kernel\_dist(i, j) = 1 - \exp^{-\frac{dist(i, j)^2}{2d_c^2}}$$ $$\rho_i = \sum_{j, i \neq j}{(1 - kernel\_dist(i, j))}$$

同时，在实现过程中并不以决策图作为判断的标准，采用论文中所实现的以$\rho_i * \delta_i$进行排序，排序后选取值较大的点作为聚类中心。

数据集在http://cs.joensuu.fi/sipu/datasets/的Shape sets处获得。除了将聚类结果可视化进行直观上的分析之外，由于数据集中含有基准聚类结果，因此可对聚类结果进行客观上的分析。在此我使用的评判标准是bcubed。 对于bcubed，假设$C_i$代表节点i的聚类类别，$L_i$代表节点i的基准类别，那么其计算公式如下

$$correctness(i, j) = bool(L_i = L_j, C_i = C_j) \\ Precision = \frac{1}{n} \sum_{i=1}^n\frac{ \sum_{C_i = C_j,i \neq j}correctness(i, j) }{ \|j | C_i = C_j, i \neq j\| } \\ Recall = \frac{1}{n} \sum_{i=1}^n \frac{ \sum_{L_i = L_j, i \neq j} correctness(i, j) }{\|j|L_i = L_j, i \neq j\|}$$

实验结果

以下是我的实现结果，在实现的同时以kmeans作为基准算法来进行比较。

Aggregation

$d_c$, dpeak precision, dpeak recall, kmeans precision, kmeans recall
2, 0.947151, 0.937514, 0.874183, 0.786176

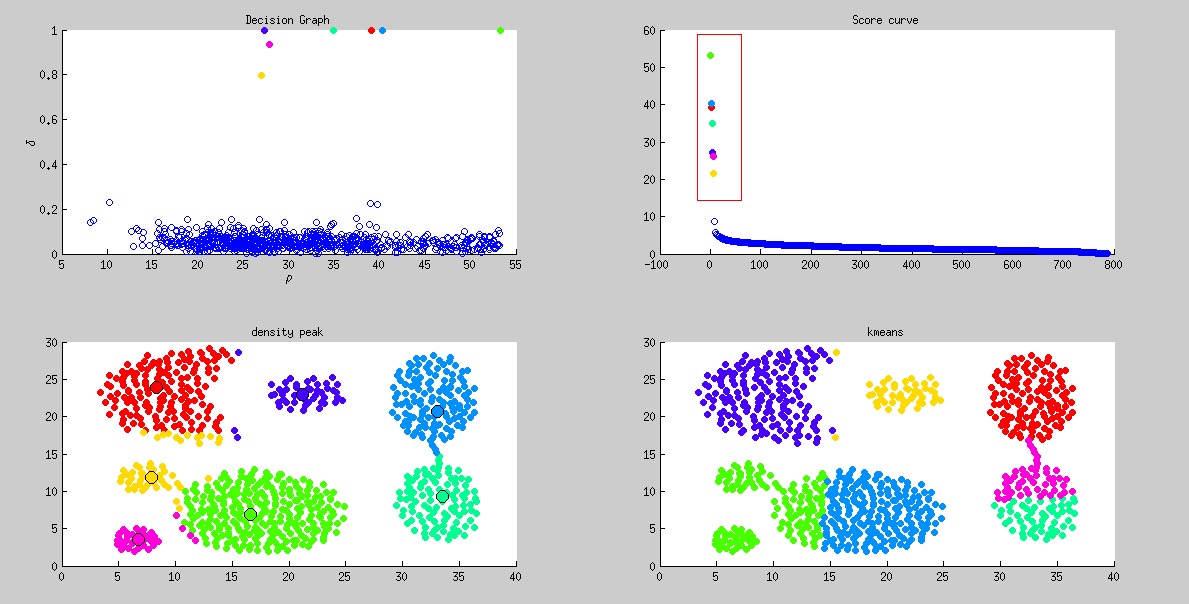
上述score curve是以$\rho_i * \delta_i$进行排序后绘制结果。其中红色框框为选取的聚类中心。

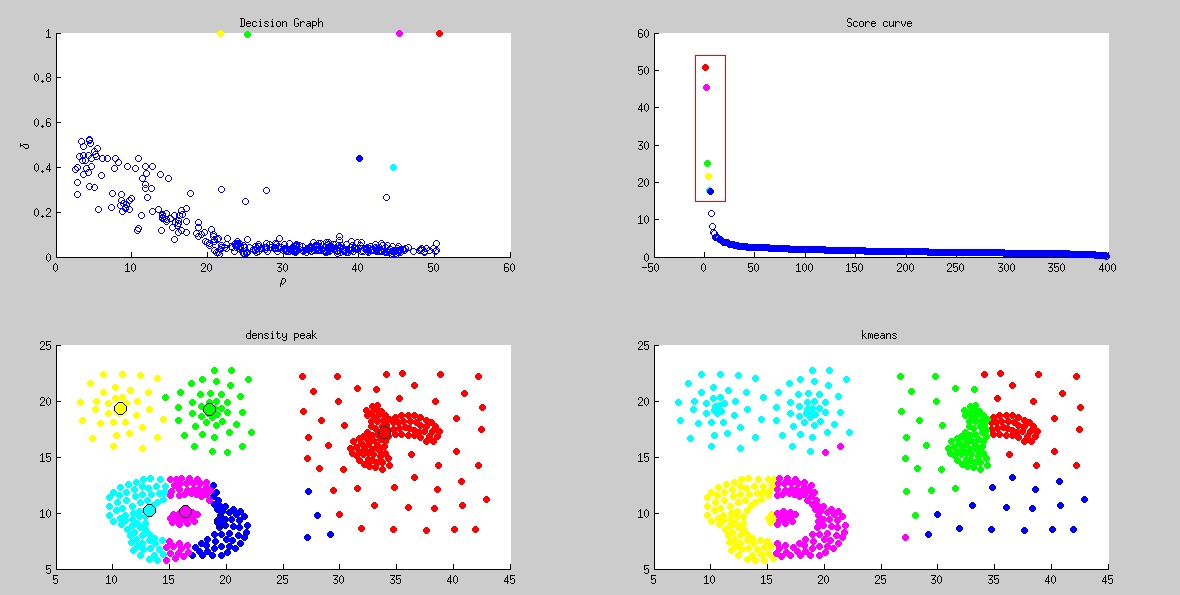
Compound

$d_c$, densitypeak bcuted precision, densitypeak bcuted recall, kmeans bcuted precision, kmeans bcuted recall
2, 0.758319, 0.713470, 0.689736, 0.581143

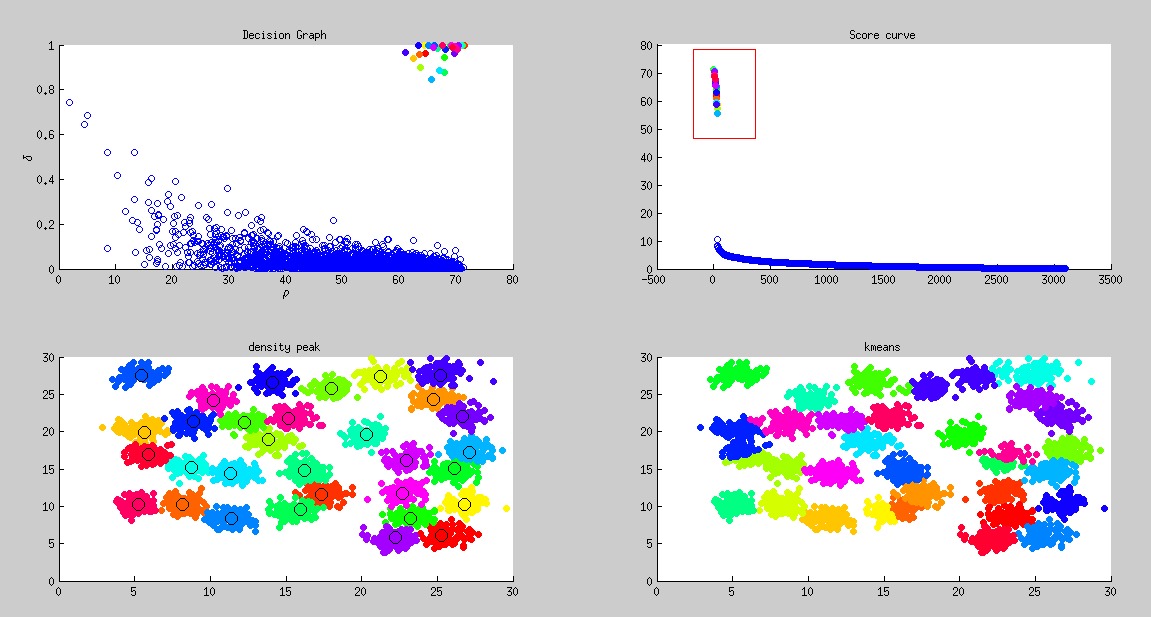
D31

$d_c$, densitypeak bcuted precision, densitypeak bcuted recall, kmeans bcuted precision, kmeans bcuted recall
1, 0.948372, 0.948485, 0.869463, 0.893978

flame

$d_c$, densitypeak bcuted precision, densitypeak bcuted recall, kmeans bcuted precision, kmeans bcuted recall
2, 0.756483, 0.736908, 0.754876, 0.735802

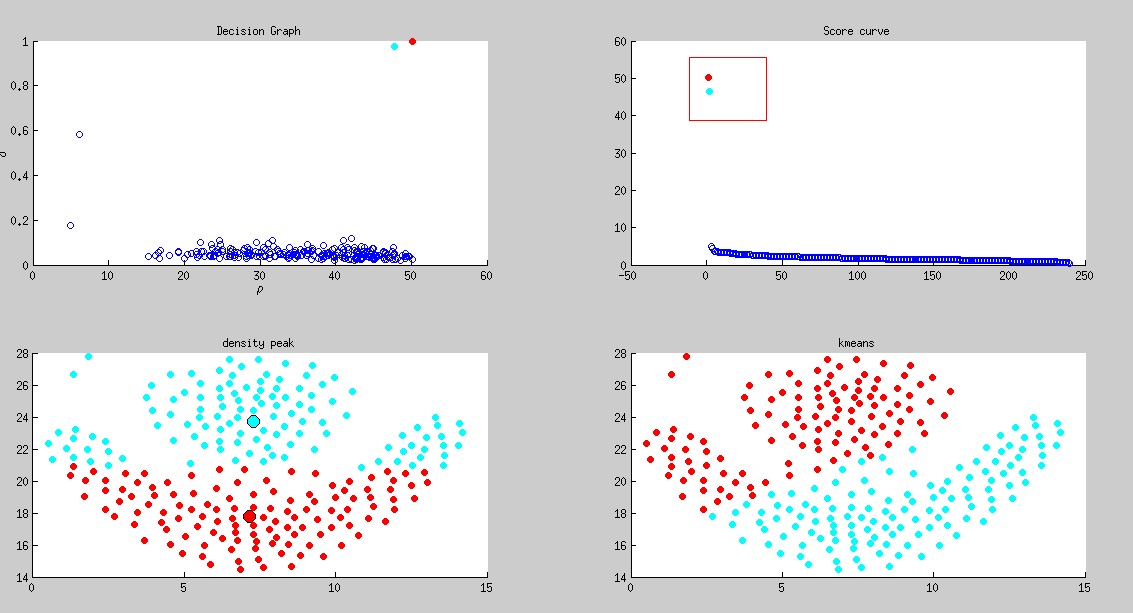
pathbased

$d_c$, densitypeak bcuted precision, densitypeak bcuted recall, kmeans bcuted precision, kmeans bcuted recall
2, 0.533395, 0.815963, 0.532796, 0.815229

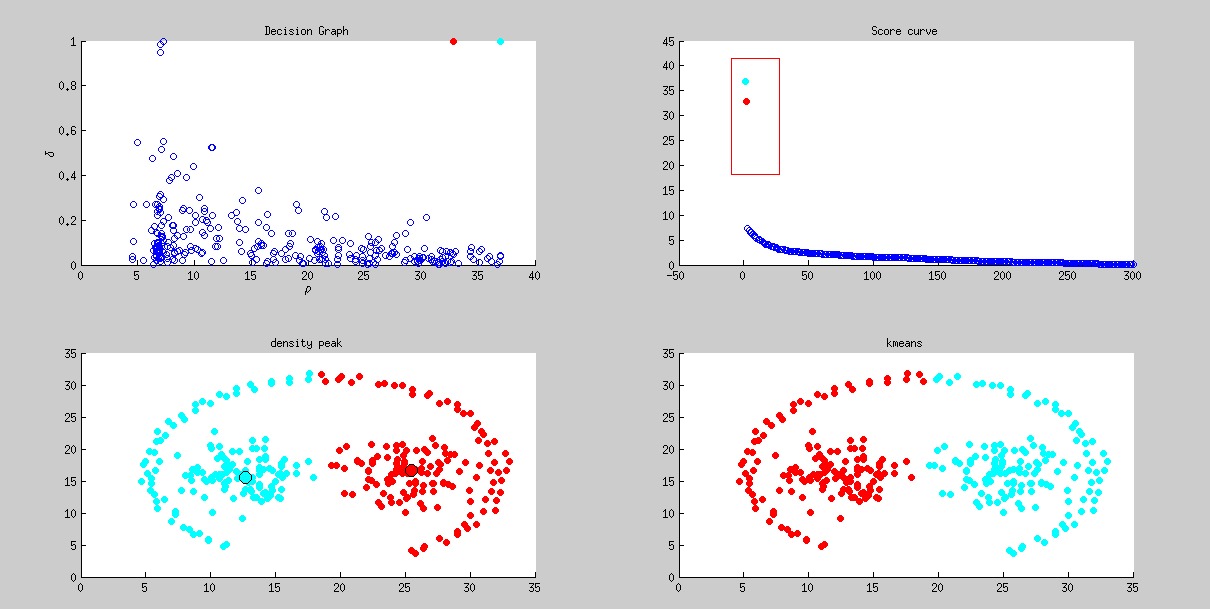
这组数据集实在太难从score curve中看出有3个聚类中心。

R15

$d_c$, densitypeak bcuted precision, densitypeak bcuted recall, kmeans bcuted precision, kmeans bcuted recall
0.7, 0.900749, 0.958974, 0.692143, 0.862222

spiral

$d_c$, densitypeak bcuted precision, densitypeak bcuted recall, kmeans bcuted precision, kmeans bcuted recall
2, 0.327694, 0.328936, 0.327500, 0.327764

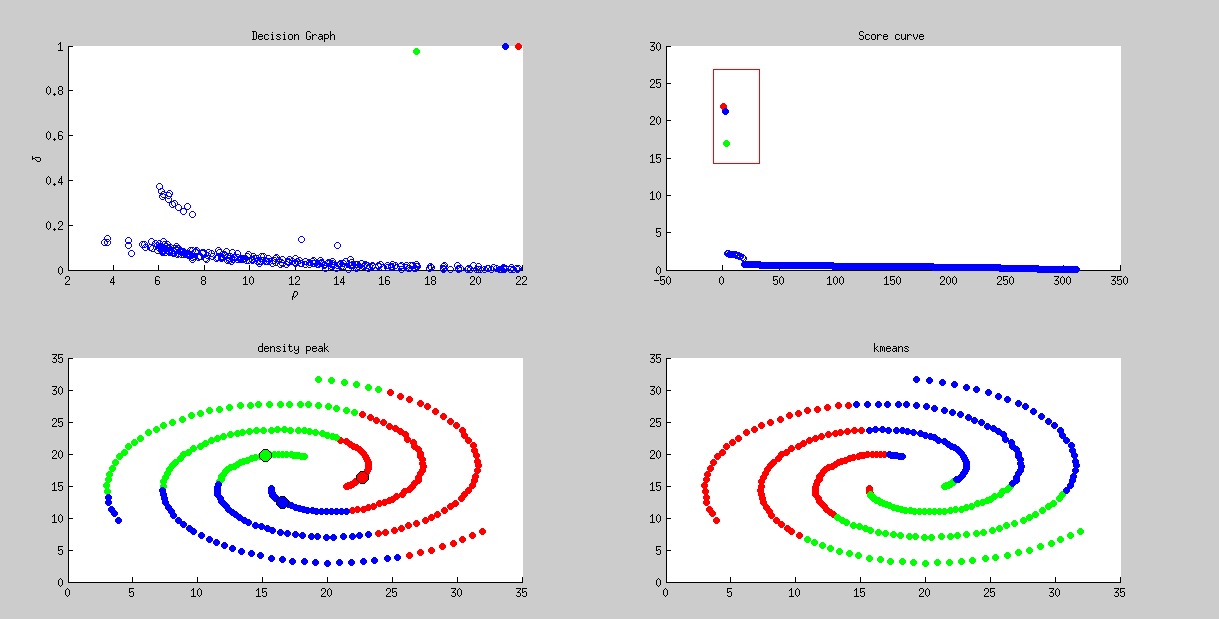
在gaussian kernel下面，无法实现出原论文中的效果。而且这组数据的表现也相当的差。一个可能原因是使用gaussian kernel的距离度量在一定程度上限制了聚类算法，这时候聚类算法更容易会把形状聚成圆形。

实验反思

这篇论文的工作非常漂亮，在这些测试数据中有很多组数据效果比kmeans好，难怪也能发表到science上。这算法在我看来有两个主要的缺点，一是人工选取聚类中心，二是$d_c$的选择并不健壮。

刚开始阅读这篇论文的时候，觉得这篇论文需要人工选择聚类中心，因此这个算法是没什么用的。后来在阅读了数据挖掘的聚类分析之后，才发现原来在聚类分析里面用到了很多启发式的方法，比如像聚类数目k的选择就是在一定程度上需要人工干预的。如果能把专业的先验知识应用到聚类分析里面，毫无疑问它能改进聚类效果，因此是非常有效的。

不过在实验过程中发现，$d_c$的选择并没有像原文中所说的那样是很鲁棒的。经常需要在不同数据集上调节$d_c$才能获得较好的效果。